include("preamble.jl")✓ file included!
using: Plots, LaTeXStrings, Polynomials, PrettyTables
Functions included:
simple_iteration,
Newton,
orderOfConvergence,
ChebyshevNodes
Use @doc <<function>> for helpinclude("preamble.jl")✓ file included!
using: Plots, LaTeXStrings, Polynomials, PrettyTables
Functions included:
simple_iteration,
Newton,
orderOfConvergence,
ChebyshevNodes
Use @doc <<function>> for helpSuppose that X = \{ x_0 < \cdots < x_n \} is a set of distinct interpolation nodes.
Aim: find p such that p(x_j) = f(x_j) for all j = 0, \dots, n.
Theorem (Lagrange Interpolation)
For x_0 < \cdots < x_n (nodes) and a function f defined on X = \{x_0,\dots,x_n\}, there exists a unique polynomial interpolant I_Xf of degree at most n such that I_Xf(x_j) = f(x_j) for all j=0,\dots,n.
In the following, we will write \mathcal P_n := \{p(x) = \sum_{j=0}^n a_j x^j \colon a_0, \dots,a_n \in \mathbb R\} for the set of polynomials of degree at most n.
N = 30
X = ChebyshevNodes(12, type=1)
Y = @. X + 100*rand()
p = fit( X, Y )
plot( p, -1, 1, label=L"y = p(x)")
scatter!( X, Y,
primary = false, markersize = 5, color="green")Theorem.
Suppose f:[a,b]\to\mathbb R is n+1 times continuously differentiable and X = \{x_0 < \dots < x_n\}. Then, for all x \in [a,b] there exists \xi_x \in [\min \{x,x_0\} , \max \{x,x_n\}] such that
\begin{align} f(x) - I_Xf(x) = \frac{f^{(n+1)}(\xi_x)}{(n+1)!} (x - x_0)(x-x_1) \cdots (x-x_n) \end{align}
In particular, we have
\begin{align} \left\| f - I_Xf \right\|_{L^\infty([a,b])} \leq \|f^{(n+1)}\|_{L^\infty([a,b])} \frac{\|\ell_X(x)\|_{L^\infty([a,b])}}{(n+1)!} \end{align}
where \ell_X(x) := (x-x_0)(x-x_1)\cdots (x-x_n) is the node polynomial and \| f \|_{L^\infty([a,b])} := \max_{x\in[a,b]} |f(x)|.
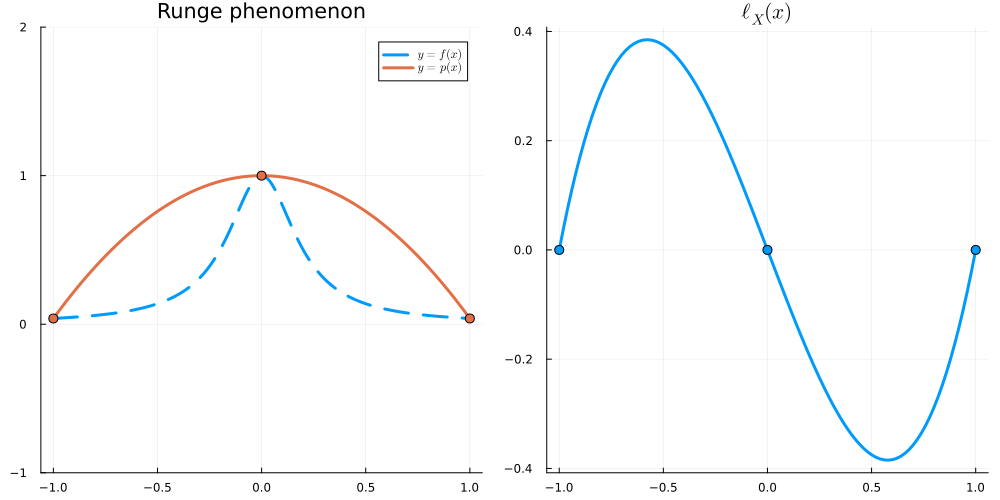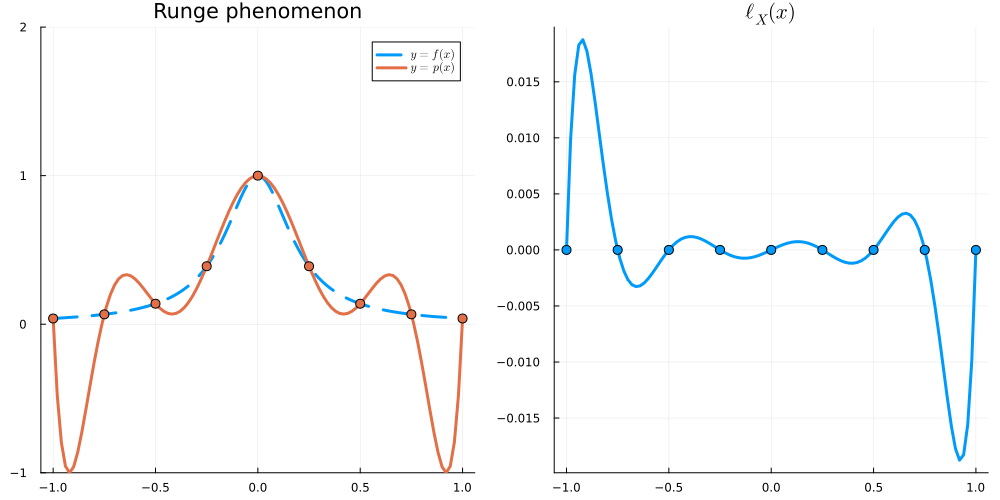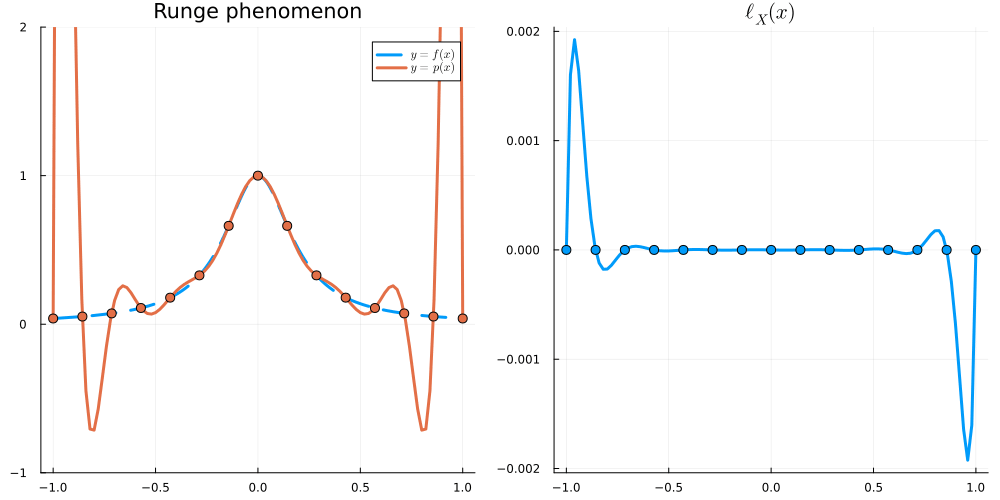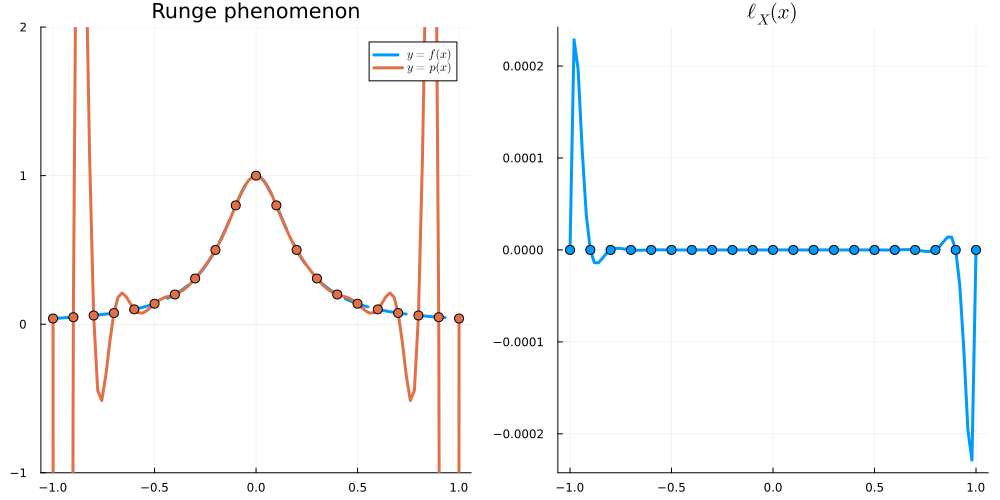
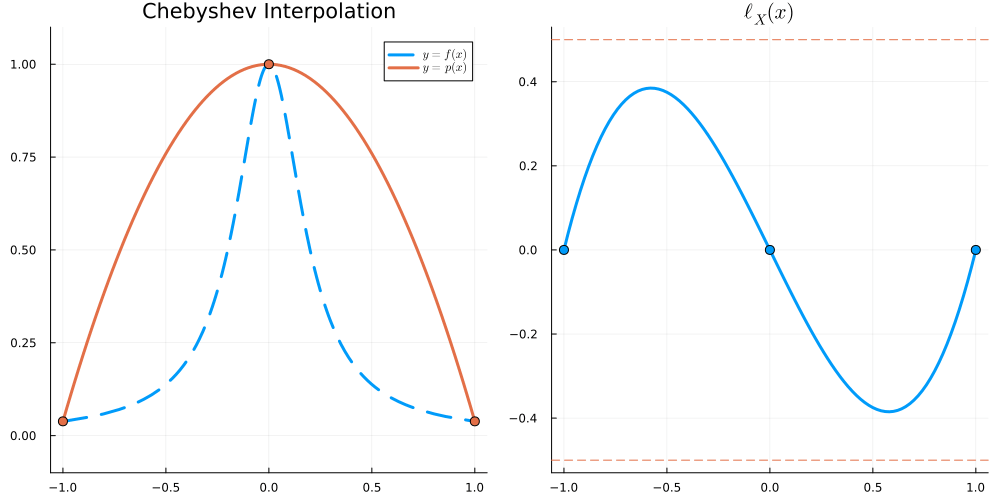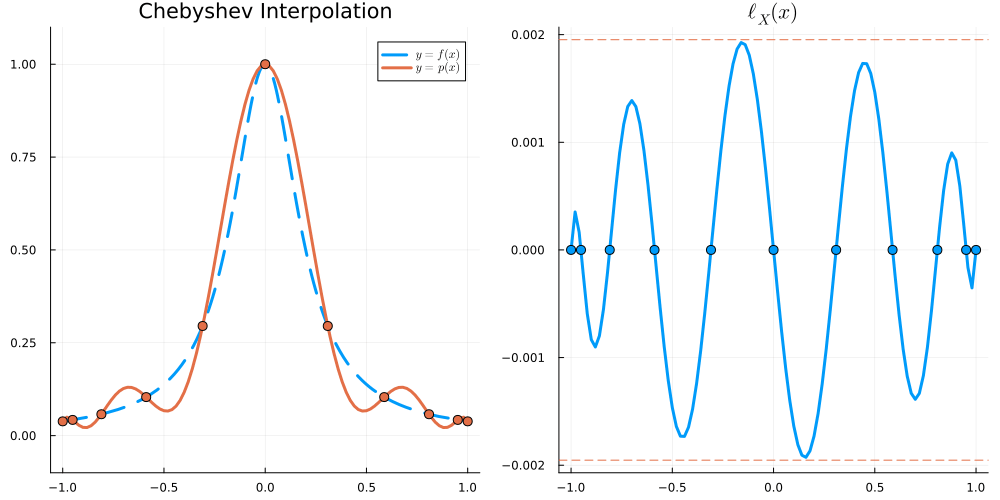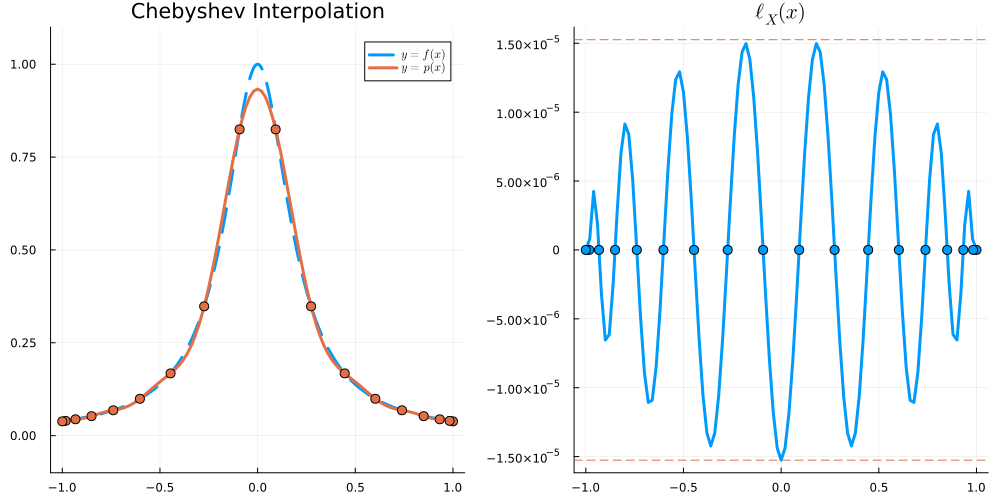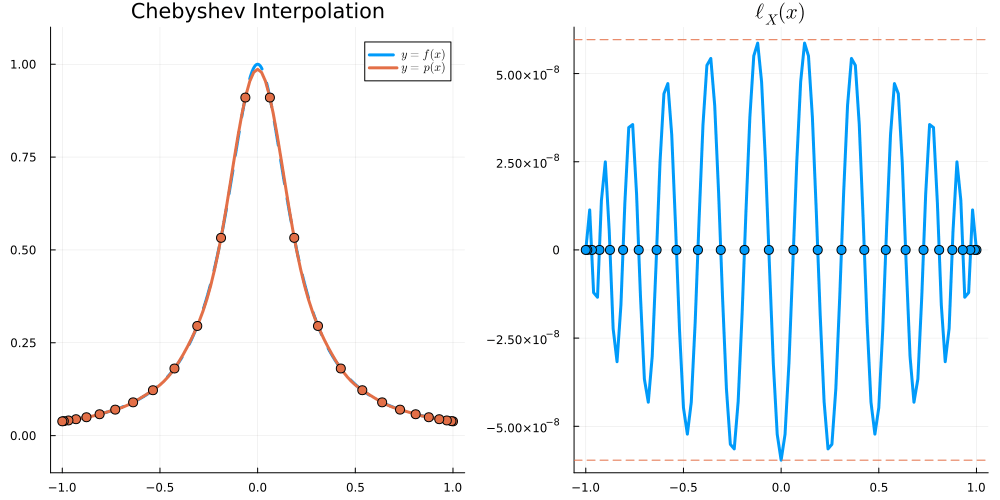
For x \in [-1,1], we have \begin{align} |\ell_X(x)| &\leq \frac{e}{2\sqrt{n}} \left( \frac2e \right)^n &\text{for Equispaced nodes } X = \Big\{ \frac{2j-n}{n} \Big\}_{j=0}^n \\ |\ell_X(x)| &\leq 2^{1-n} &\text{for Chebyshev nodes } X = \Big\{ \cos \frac{j\pi}{n} \Big\}_{j=0}^n \end{align}
In this section, we will write \| f \|_{L^\infty} := \max_{x \in [-1,1]} |f(x)|.
Recall that
\begin{align} \left\| f - I_Xf \right\|_{L^\infty} \leq \frac{\|f^{(n+1)}\|_{L^\infty}}{(n+1)!} \|\ell_X\|_{L^\infty} \end{align}
so it is natural to want to minimise
\begin{align} \|\ell_X\|_{L^\infty} = \max_{x \in [-1,1]} |(x-x_0)(x-x_1)\dots(x-x_n)| \end{align}
over all choices of X = \{x_0,\dots,x_n\}. Equivalently, we are minimising \| p \|_{L^\infty} over all monic polynomials p of degree n+1: that is, over all p such that p(x) = x^{n+1} + q(x) with q\in \mathcal P_n. We will show that scaled Chebyshev polynomials (of the first kind) solve this (so-called Chebyshev) problem.
For x \in [-1,1] there exists \theta \in [0,\pi] such that x = \cos\theta. We can therefore define T_n on [-1,1] by the condition that
\begin{align} T_n( \cos \theta ) = \cos n\theta. \end{align}
for n = 0,1,2,....
We define X_{\mathrm{I}} to be the set of n+1 zeros of T_{n+1} and X_{\mathrm{II}} to be the set of n+1 extreme points of T_n.
\begin{align} X_{\mathrm I} &= \Big\{ \cos \frac{(2j+1)\pi}{2(n+1)} \Big\}_{j=0}^{n} \nonumber\\ X_{\mathrm{II}} &= \big\{ \cos\tfrac{j\pi}{n} \big\}_{j=0}^n \end{align}
X_{\mathrm{I}} and X_{\mathrm{II}} are the Chebyshev nodes of the first and second kind, respectively.
Here, we plot the first 5 Chebyshev polynomials on [-1,1] together with (x, T_n(x)) for x \in X_{\mathrm{II}} with n=5
plot(ChebyshevT([1.]), -1, 1, title="Chebyshev I", legend = false, lw = 3)
plot!(ChebyshevT([0, 1]), -1, 1, title="Chebyshev I", legend = false, lw = 3)
plot!(ChebyshevT([0,0,1.]), -1, 1, title="Chebyshev I", legend = false, lw = 3)
plot!(ChebyshevT([0,0,0,1.]), -1, 1, title="Chebyshev I", legend = false, lw = 3)
plot!(ChebyshevT([0,0,0,0,1.]), -1, 1, title="Chebyshev I", legend = false, lw = 3)
p = ChebyshevT([0,0,0,0,0,1.])
plot!(p, -1, 1, title="Chebyshev I", legend = false, lw = 3)
scatter!( @. cos( pi*(0:5)/5 ), @. p( cos( pi* (0:5)/5 ) ) )We define the monic (with leading coefficient equal to 1) Chebyshev polynomials as t_0(x) = 1 and t_n(x) := 2^{1-n} T_n(x) for n \geq 1. We are ready for the main result of this section (“Which nodes to choose?”):
Theorem.
The monic Chebyshev polynomials solve the Chebyshev problem (on [-1,1]). That is,
\begin{align} \|t_{n+1} \|_{L^\infty([-1,1])} = \min_{p = x^{n+1} + q : \,\, q \in \mathcal P_n } \big\| p \big\|_{L^\infty([-1,1])}. \end{align}
We have therefore shown that, choosing X =X_{\mathrm{I}}= \{ \text{zeros of }t_{n+1} \} minimises the node polynomial in the following sense
\begin{align} \min_{ y_0 < \dots < y_n } \| \ell_{Y} \|_{L^\infty([-1,1])} \geq \| \ell_X \|_{L^\infty([-1,1])} = 2^{-n} \end{align}
It turns out that \ell_{X_{\mathrm{II}}}(x) = 2^{-n} \big( T_{n+1}(x) - T_{n-1}(x) \big) and so \|\ell_{X_{\mathrm{II}}}\|_{L^\infty([-1,1])} \leq 2^{1-n} (here, we used |T_{n}|\leq 1) and so, in practice, one expects the same approximation rates when using X = X_{\mathrm{II}} = \{\text{extreme points of } T_n \}.
Using the standard Lagrange formulation p(x) = \sum_{j=0}^n \ell_j(x) f(x_j) is slow and unstable! Computing \ell_j(x) for a single x requires O(n) operations and thus evaluating p(x) requires O(n^2). Moreover, due to subtractive cancellation, this method is unstable.
n = 1000
x = @. cos( π*(0:n)/n )
y = @. Runge( x )
function L( j, t )
if j == 0
return prod( @. t - x[2:end] ) / prod( @. x[1] - x[2:end] )
elseif j == length(x)-1
return prod( @. t - x[1:end-1] ) / prod( @. x[end] - x[1:end-1] )
else
return prod( @. t - x[1:j] ) * prod( @. t - x[(j+2):end] ) / ( prod( @. x[j+1] - x[1:j] ) * prod( @. x[j+1] - x[(j+2):end] ) )
end
end
function p_naive( t )
r = 0
for j in 0:(length(x)-1)
r = r + L(j, t ) * y[j+1]
end
return r
end
plot(Runge, -1, 1, label=L"y = f(x)", lw = 3, linestyle = :dash, legend=false)
@time plot!( t -> p_naive( t ), -1, 1, title="Naive implementation: slow/unstable", lw = 3 )
scatter!( [x], [Runge.(x)]) 11.514745 seconds (25.91 M allocations: 15.135 GiB, 19.87% gc time, 4.09% compilation time)Instead, we may use the Barycentric formula: First notice that
\begin{align} \ell_j(x) = \prod_{k \not= j} \frac{x - x_k}{x_j - x_k} = \frac{\ell_X(x)}{x- x_j} \frac{1}{ \prod_{k \not= j} (x_j - x_k) } \end{align}
Therefore on defining \lambda_j := \left( \prod_{k \not= j} (x_j - x_k) \right)^{-1} and dividing by \sum_{j=0}^n \ell_j(x) = 1, we obtain
\begin{align} p(x) &= \left. \sum_{j=0}^n \ell_j(x) f(x_j) \middle/ \sum_{j=0}^n \ell_j(x) \right. \nonumber\\ &= \left. \ell_X(x) \sum_{j=0}^n \frac{\lambda_j f(x_j)}{x - x_j} \middle/ \ell_X(x) \sum_{j=0}^n \frac{\lambda_j}{x - x_j} \right. \nonumber\\ &= \left. \sum_{j=0}^n \frac{\lambda_j f(x_j)}{x - x_j} \middle/ \sum_{j=0}^n \frac{\lambda_j}{x - x_j} \right. \end{align}
which is known as the Barycentric Formula.
For a fixed interpolation set, one may compute \lambda_j once and then evaluating p(x) requires only O(n) computations.
In fact, for the Chebyshev nodes X_{\mathrm{II}} = \big\{ \cos \frac{j\pi}{n} \big\}_{j=0}^n, we have a simple formula for the \lambda_j:
\begin{align} \lambda_j = \begin{cases} \frac{2^{n}}{4n} & \text{if } j = 0\nonumber\\ (-1)^j \frac{2^{n}}{2n} & \text{if } j = 1,\dots,n-1 \nonumber\\ (-1)^n \frac{2^{n}}{4n} & \text{if } j = n \end{cases} \end{align}
Moreover, this formula has been proved to be numerically stable which we demonstrate in the following:
p_bary = ChebyshevInterpolant( Runge, 1000 )
plot(Runge, -1, 1, label=L"y = f(x)", lw = 3, linestyle = :dash, title = "Barycentric formula")
plot!(p_bary, -1, 1, label=L"y = p(x)", lw = 3 )
scatter!( [x], [Runge.(x)], primary = false)FIx X = \{x_0, x_1, \cdots, x_{n} \}. Newton polynomials are the node polynomials corresponding to the first nodes in X:
\begin{align} \pi_0(x) &= 1 \nonumber\\ \pi_1(x) &= \ell_{\{x_0\}}(x) = (x - x_0) \nonumber\\ \pi_2(x) &= \ell_{\{ x_0, x_1 \}}(x) = (x - x_0)(x-x_1) \nonumber\\ \vdots \nonumber\\ \pi_n(x) &= \ell_{\{ x_0, x_1, \dots, x_{n-1} \}}(x) = (x-x_0)(x-x_1)\cdots (x-x_{n-1}) \end{align}
Example.
We computed the Lagrange interpolation of f(x) = \sin x on X = \{ 0, \frac\pi2, \pi \}.
f = x->sin(x)
x = [0, pi/2, pi]
y = f.(x)
p = fit(x,y)
plot(f, -2pi, 2pi, label=L"y = \sin x", lw=2, linestyle=:dash)
plot!( p, xlims=(-2pi,2pi), label=L"y= p(x)", lw=3)
scatter!( x, y, markersize=5, primary=false)Write down the Newton form of this polynomial interpolant.
q = (2/π)* Polynomial([0,1,]) - (4/pi^2) * Polynomial( [0, -pi/2, 1] )
plot!(q, xlims=(-2pi,2pi), label=L"y=q(x)")Notice that if p interpolates f at X = \{x_0,\dots,x_n\} and the x_j are distinct, then
\begin{align} p(x) &= a_0 + a_1 (x - x_0) + a_2 (x-x_0)(x-x_1) + \cdots + a_n (x-x_0)(x-x_1) \cdots (x - x_{n-1})\nonumber\\ % &= f(x_0) + \frac{f(x_1) - f(x_0)}{x_1 - x_0} (x-x_0) + a_2 \pi_2(x) + \cdots + a_n \pi_n(x) \end{align}
Definition.
We define the divided difference f[x_{0}, \dots, x_n] to be the leading cofficient in the polynomial interpolation p\in \mathcal P_n of f on the set of distinct nodes X = \{x_0,x_1,\dots, x_n\}: that is,
\begin{align} p(x) = f[x_0,\dots,x_n] x^n + q(x) \end{align}
where q \in \mathcal P_{n-1}.
We have seen that f[x_0] = f(x_0) and f[x_0,x_1] = \frac{f(x_1) - f(x_0)}{x_1 - x_0}. (Here, we just solved p(x_0) = f(x_0) and p(x_1) = f(x_1)).
Lemma.
The divided difference f[x_{0}, \dots, x_n] doesn’t depend on the ordering of the interpolation nodes. Moreover, we have linearity: (f + c g)[x_0,...,x_n] = f[x_0,...,x_n] + c g[x_0,...,x_n].
Proof.
The polynomial interpolant p\in \mathcal P_n of f on X is independent of the ordering of the nodes.
Moreover, if p and q are the polynomial interpolants of f and g, respectively, then p + c q is a polynomial interpolant of f+ c g.
Theorem.
Suppose X = \{x_0,\cdots,x_n\} is a set of n+1 distinct interpolation nodes. Then, we have the recursion
\begin{align} f[x_0, \dots, x_n] &= \frac {f[x_1, \dots, x_n] - f[x_0, \dots, x_{n-1}]} {x_n - x_1} \end{align}
Let’s go back to interpolating f(x) =\sin x on \{0, \frac\pi2, \pi\}. Now add -2\pi as an interpolation node and compute the new polynomial interpolant.
We compute the divided difference table:
\begin{align} &x_0 = 0, \quad &f[x_0] = 0, \qquad &f[x_0,x_1] = \frac{f[x_1] - f[x_0]}{x_1 - x_0} = \frac{2}\pi, \quad &f[x_0,x_1,x_2] = \frac{f[x_1,x_2] - f[x_0,x_1]}{x_2 - x_0} = -\frac{4}{\pi^2} \nonumber\\ % &x_1 = \tfrac\pi2, \quad &f[x_1] = 1, \qquad &f[x_1,x_2] = \frac{f[x_2] - f[x_1]}{x_2 - x_1} = -\frac{2}\pi, \quad &f[x_1,x_2,x_3] = \frac{f[x_2,x_3] - f[x_1,x_2]}{x_3 - x_1} = -\tfrac{4}{5\pi^2} \nonumber\\ % &x_2 = \pi, \quad &f[x_2] = 0, \qquad &f[x_2,x_3] = \frac{f[x_3] - f[x_2]}{x_3 - x_2} = 0 \quad & \nonumber\\ &x_3 = -2\pi, \quad &f[x_3] = 0, \qquad & \quad & \quad &\nonumber \end{align}
The final entry on the top row is
\begin{align} f[x_0,x_1,x_2,x_3] &= \frac{f[x_1,x_2,x_3] - f[x_0,x_1,x_2]}{x_3 - x_0} = - \frac{ 8 }{ 5 \pi^3 } \nonumber \end{align}
and so
\begin{align} p(x) = 0 + \frac{2}\pi x - \frac{4}{\pi^2} x \big(x - \tfrac\pi2\big) - \frac{ 8 }{ 5 \pi^3 } x\big(x - \tfrac\pi2)\big(x - \pi\big) \nonumber \end{align}
We plot this below:
r = x-> - 4*x*(x-pi)/pi^2 - 8*x*(x-pi/2)*(x-pi)/(5*pi^3)
x = [0, pi/2, pi, -2pi]
y = f.(x)
plot(f, -2pi, 2pi, label=L"y = \sin x", lw=2, linestyle=:dash)
plot!( p, xlims=(-2pi,2pi), label=L"y= p_2(x)", lw=3)
plot!( r, xlims=(-2pi,2pi), label=L"y= p_3(x)", lw=3)
scatter!( x, y, markersize=5, primary=false)Proof.
We will now prove the recursive formula. Let p \in \mathcal P_{n-1} be the polynomial interpolation of f on X = \{x_0,\dots, x_{n-1}\} and define g(x) = (x-x_{n})f(x) for some fixed x_{n} \not\in X. Then, g(x) and q(x) := (x - x_{n}) p(x) agree on x_0,...,x_{n-1}, x_{n} and so q is the polynomial of least degree interpolating g on X \cup \{x_{n}\}. Therefore, the leading coefficient of q(x) = (x - x_{n}) p(x) is both g[x_0,\dots,x_{n}] (because q interpolates g on X \cup \{x_{n}\}) and f[x_0,\cdots,x_{n-1}] (because q is (x-x_{n}) times p). That is, g[x_0,...,x_{n}] = f[x_0,...,x_{n-1}].
That is, we have \big( (x - x_n) f \big) [x_0,\dots,x_n] = f[x_0,\dots,x_{n-1}]. By relabeling the indices (which is allowed because f[x_0,\dots,x_n] does not depend on the ordering of the interpolation nodes), we also have \big( (x - x_0) f \big) [x_0,\dots,x_n] = f[x_1,\dots,x_{n}]. Therefore, by linearity we have
\begin{align} (x_n - x_0) f[x_0,\dots,x_n] &= \big( (x - x_0) f - (x-x_n) f \big) [x_0,\dots,x_n] \nonumber\\ % &= \big( (x - x_0) f \big) [x_0,\dots,x_n] - \big( (x-x_n) f \big) [x_0,\dots,x_n] \nonumber\\ % &= f [x_1,\dots,x_n] - f [x_0,\dots,x_{n-1}] \nonumber \end{align}
Now consider the multiset X = \{\{ x_0, x_1, \dots, x_{n} \}\} where x_j appears m_j \geq 1 times in X.
Hermite: find p such that
\begin{align} p(x_j) = f(x_j), &\quad p'(x_j) = f'(x_j), &\quad ... &\quad p^{(m_j-1)}(x_j) = f^{(m_j-1)}(x_j). \end{align}
Exercise.
What is the least degree polynomial interpolant on X = \{x_0, x_0, x_0, \cdots, x_0\}?
Theorem.
There exists a unique polynomial of degree at most n solving the Hermite interpolation problem.
Again, we define the divided differences (but now for the more general case where we may have repeated interpolation nodes):
Definition.
We define the divided difference f[x_{0}, \dots, x_n] to be the leading cofficient in the polynomial interpolation p\in \mathcal P_n solving the Hermite interpolation problem for f on X:
\begin{align} p(x) = f[x_0,\dots,x_n] x^n + q(x) \end{align}
where q \in \mathcal P_{n-1} and p^{(l)}(x_j) = f^{(l)}(x_j) for l = 0,\dots,m_j-1.
Theorem.
We have
\begin{align} f[x_0, \dots, x_n] &= \begin{cases} \frac{f^{(n)}(x_0)}{n!} & \text{if } x_0 = x_1 = \dots = x_n \\ \frac {f[x_1, \dots, x_n] - f[x_0, \dots, x_{n-1}]} {x_n - x_1} &\text{otherwise} \end{cases} \end{align}
Proof.
You have seen above that the Taylor polynomial
\begin{align} T_f(x) =\sum_{j=0}^n \frac{f^{(j)}(x_0)}{j!}(x - x_0)^j \end{align}
solves the Hermite interpolation problem on X = \{\{x_0,\dots,x_n\}\} in the case where x_0 = \dots = x_n. For such X, the leading coefficient in this expression is f[x_{0}, \dots, x_n] = \frac{f^{(n)}(x_0)}{n!}.
One can adapt the proof of the recursive formula that we had for distinct interpolation nodes to this case [exercise].
Exercise.
What is the Hermite interpolant of f(x) = \sin x on \{\{ 0,0,\pi, \pi\}\}? Hint: you can compute the divided difference tables in the same way as before.